線分AB上に点Cを、
AC:BC=AB:AC
となるようにとったとき、ACとBCの比を黄金比といい、値は、1.61803398875..... : 1となります。これを簡単な整数比に近似すると、5 : 3 あるいは 8 : 5 となります。
黄金比は、フィボナッチ数列の隣接2項の比の極限値としても得られ、また、2次方程式x^2-x-1=0またはx^2+x-1=0の正の解としても得られます。
古来、美しいプロポーションとして重要視され、中世ヨーロッパでは、神聖比例(Divine Proportion)とも呼ばれました(『神聖比例』フラ・ルカ・パチオリ、ca.1450-ca.1520)。
近代にいたって、ル・コルビュジエは、形づくりの論理として黄金比に着目し、フィボナッチ数列を人体に適用したモデュロ−ルを提唱しました。
いろいろな文献における黄金比の説明
『形のデータファイル』・『広辞苑』・『建築美論の歩み』・『建築大辞典』・新潮社『世界美術事典』
簡単な作図の方法
黄金比は無理数なので、定規で測って描くことはできません。
簡単な整数比に近似すると 3 : 5 あるいは5 : 8 となるので、この値を使う方法もありますが、定規とコンパスがあれば、簡単に、正確に作図できます。(->作図のアニメーション)
|
|
|
正方形を描く。 |
|
|
|
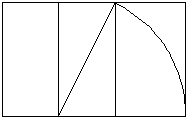
2分割する。 |
|
|
|
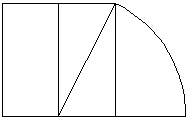
2分割した長方形の対角線を半径とする円弧を描く。 |
|
|
|
円弧を含む長方形を描けば、出来上がり。 |